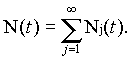 |
(3) |
and
Bracewell suggests [1] that extraterrestrial technological civilizations
might use automated probes for interstellar exploration and communication,
rather than radio waves. This approach receives support from Freitas [2-4], who
proposes a balanced programme of SETI research which includes a search for
xenological artifacts residing in the Solar System. Following this proposal,
Freitas and Valdes [5] undertook a preliminary photographic investigation of the
Earth-Moon triangular libration points L4 and L5 and the solar-synchronized
positions in the associated halo orbits. The engineering feasibility of
interstellar probe flyby missions has been examined and favourably reported by
members of the British Interplanetary Society [6].
Freitas [2] suggest a major alternative to one-shot parking-orbit "Bracewell
probes" and stellar flyby "Daedalus probes" - the self-reproducing interstellar
probe. The plausibility and engineering feasibility of such a device are
considered in some detail, with the conclusion that a generation time of
~103 years is possible assuming a 10-fold improvement in current
human space/manufacturing technology. In the present paper the authors compare
reproducing and nonreproducing strategies for missions of galactic exploration.
Self -reproducing probes are found to be the method of choice for active
programmes lasting > 104 years and involving searches of >
106 target stars to distances > 1000 light-years in the Galactic
Disk, and are superior to one-shot "Bracewell probes" for searches of >
103 stars to distances > 100 light-years in the Galactic Disk.
The history of the jth starprobe is as
follows. The interstellar exploration program begins at t0. At t1
= t0 + jt , where t is the probe construction time,
the jth vehicle has been built and is
launched. At t2 = t1 + rj -
D)/V, where V is the average interstellar cruise velocity and D = r-1/3 is the mean interstellar distance, the
jth probe begins transmitting its first report. At t3 = t2 +
rj/c, where c
is the speed of light, the sending society begins to receive the first report.
By
When the probe has examined all n stars for which it is responsible, tn+3 = t3 + n(D/V+a) and the sending civilization has received n reports. The activities of the jth probe then terminate.
Following the exploration scenario detailed above, the number of reports on alien solar systems received by the sending civilization from the jth probe at time t, Nj(t), is given by
|
|
(1) |
| ? | 0, x < 0 | ||
| R(x) = ? |
(2) | ||
| ? | x, x >= 0. |
The total number of complete reports received by the sending civilization, N(t), is obtained by summing Nj(t) for all j, or
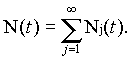 |
(3) |
Note that the use of the ramp function in defining Nj(t) permits N(t) to be written as an infinite sum, hence the exploration model is strategy - independent.
The exact location and topological configuration of each search cell, designed for maximum exploration efficiency, requires a detailed analysis which lies beyond the scope of this paper. Instead, a shell approximation is used in which cells are ordered with sequentially increasing radii slsuch that a sphere of radius se contains exactly nl+1 stars. The lth cell then has a radius given by
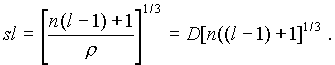 |
(4) |
The term "shell approximation" does not mean probes actually investigate an entire spherical shell; rather, they are treated as exploring a cell of unspecified shape at a distance slfrom the home star.
|
|
(5) |
In the Expanding Shell Strategy, the arguments of the ramp functions used in Eqn. 11) may be written as
|
|
(6) | |
|
|
(7) |
The ramp functions are eliminated from Eqn. [3] by summing R(t - t3) from j = 1 to J. where, for j <= Jmax, (t - t3) is non-negative, and summing R(t - tn+3) from j = 1 to J'max where, for j <= J'ma, (t - tn+3) is non-negative. Thus Eqn. [3] becomes
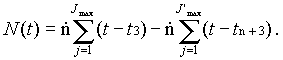 |
(8) |
The Jmax and J'max are calculated by setting (t - t3)=0 and (t - tn+3) = 0 in Eqns. [6] and [7], respectively, and solving the resulting cubic equations for j = Jmax in Eqn. [61 and j = J'max in Eqn. [7]. Combining Eqns. [6], [7], and [8], and explicitly evaluating the sums,
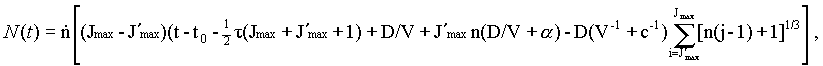 |
(8) |
for all Jmax ? 1 and all J'max ? 1. Note that if J'max < 1 then J'max is zero in Eqn. [9]
Results based on Eqn.
[9] are presented in Section
4.
A self -reproducing starprobe, described by Freitas [2], enters a target
star system, selects and lands upon a suitable rocky moon of a jovian planet,
then in a period of 500 years constructs a giant factory complex which itself is
able to build one exact copy of the original machine every 500 years thereafter.
In the exploration model discussed here, the sending civilization launches just
one self-reproducing probe. The original device is designed for an effective
lifespan of G reproductive cycles or "generations,"
and is itself considered to be the 0th generation. Each parent machine produces
in offspring at a rate of b-1
yr-1, which for simplicity is taken as 500(l+m-1) years in
order to amortize the time delay due to factory construction over the entire
crop of offspring. During its lifetime each probe explores only one target star.
In the self-reproducing starprobe model of galactic exploration, the stellar distribution again is taken to be infinite and homogeneous, with a number density r of target stars of mean separation D = r-1/3. The designated exploration space is partitioned into a small number (m) of large equal-volume supercells. Each daughter probe is assigned a supercell, which it may further subdivide and delegate in parcels to subsequent generations of its daughters.
The history of starprobe P(j0, j1, ..., jg) of the gth generation, which jj is birth order in the ith generation, follows a specific sequence. The exploration program begins at to. At t0 + t the original self -reproducing probe is built and launched. At tj0 = t0 + t + rj0 (V-1 + c-1) + a, where rj0 = D is the distance to the nearest target star, the original probe arrives at its destination and reports back., At til = tj0 + j1b + rj1 (V-1 + c-1) + a, the firstgeneration ancestor of probe P is built, launched to a target star in the j1st exploration supercell, and reports to its parent who relays the information back to the sending civilization. At tig = tig_1 + jgb + rjg (V-1 + c-1) + a, the gth-generation offspring with birth order jg, probe P, is built, arrives at its assigned target star, and reports back through the chain of ancestral parental repeater stations. (P may continue to reproduce if g < C.) Reports are made through earlier generations for mathematical simplicity.
If N(t) is the total number of reports received by the sending civilization at time t from all generations and offspring of the original starprobe, then
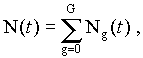 |
(10) |
where Ng(t) is the sum of all reports received from all members of the gth generation. Ng(t) may be written as
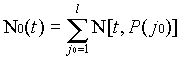 |
(11) | |
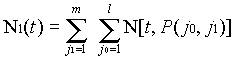 | ||
|
. . | ||
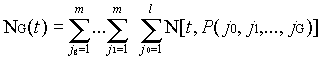 |
for g = 0, ..., G, where N[t, P] is the number of reports received from probe P by time t. N[t, P] may be expressed in terms of the Heaviside operator
| ? 0 x < 0
H(x) = ? ? 1 x ? 0 |
(12) |
as
|
|
(13) |
where tjg is the time at which probe P's report is received by the sending civilization.
The possible strategies that might be used to deploy a large fleet of self -reproducing exploratory craft are virtually infinite. Optimization calculations are particularly intractable in this case. For these reasons we again consider a single strategy which can be evaluated with relative ease.
In the Telescoping Shell Strategy, the 0th generation probe is sent to the target star nearest the sending civilization, a distance D away. Since m and G are fixed by probe design, the original machine and its descendants can explore a total of N* stars, where
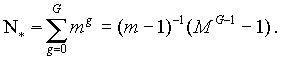 |
(14) |
A fixed exploration sphere surrounding the first target star contains N* - 1 stars, excluding home and target. The
sphere is divided into m shells each containing (N* - l)/ m stars, and each of the m
first -generation daughter probes is assigned to a target star in each shell.
For mathematical simplicity, the (N*
-1)/m stars in each first-generation shell
subsequently are regarded as having spherical distribution. These subspheres
each contain (N* - 1)/m - 1 suns, again excluding the target, Every second
-generation daughter probe is assigned to a subsphere shell containing 1/mth of this total, or ((N* - 1)/m - 1)/ m = (N* - m - l)/m2 stars. The
gth-generation daughter probes are assigned to subsphere shells
containing m-g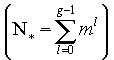 stars. This process of telescoping subspheres continues
until each daughter in the Gth generation is assigned to an isolated target star
and all N* targets have been explored.
stars. This process of telescoping subspheres continues
until each daughter in the Gth generation is assigned to an isolated target star
and all N* targets have been explored.
If rji is the separation between the jith daughter of the ith generation and its parent probe, then:
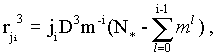 |
(15) |
or
|
|
(16) |
for i ? 1. Hence the receipt time of probe P's report may be written:
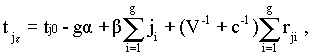 |
(17) |
and N[t,P] in Eqn. [13] may be calculated for any P, given t.
The objectives of a program to explore N(t)
stars are achieved most efficiently when the program duration T and the level of technological sophistication in the
original starprobe both are held to a minimum. Technical sophistication is
minimized when 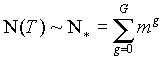 , as this condition ensures that no unnecessary daughter probes
will be built. The program duration T is
minimized by selecting m and G such that, for G ? 1 and m ? 2,
, as this condition ensures that no unnecessary daughter probes
will be built. The program duration T is
minimized by selecting m and G such that, for G ? 1 and m ? 2,
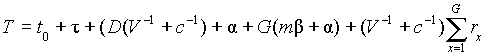 |
(18) |
|
|
(19) |
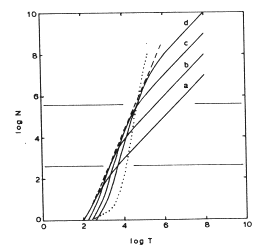
Fig. 1. Comparison of the number of stars explored N(T) as a function of the exploration period T, for nonreproducing probes (solid curves) with (a) n = 1, (b) n = 10, (c) n = 100, and (d) n = 1000, and for reproducing probes (dotted curve). The optimal nonreproducing curve is indicated by the dashed line. The stellar density adopted is r = 4.3 x 10-4 stars ly-3, probe velocity is V = 0.1c, and the residence time is a = 1 yr. For the nonreproducing model t = 10 yrs, and for the reproducing model t = 100 yrs and b = 500 (1 + m-1) yrs. The horizontal fines demarcate programme exploration ranges of 100 ly and 1000 ly in the Galactic Disk.
The Strategies formulated for each model of interstellar exploration are
evaluated numerically. Habitable star systems are taken roughly as 10% of all
stellar classes [7, 8], so the number density r is 4.3?
10-4 stars ly-3 in the Galactic Disk population, 8.7? 10-3 stars ly-3 in the Outer Core
region of the Galaxy and 6.6? 10-3 stars
ly-3 in the Halo. The mean interstellar cruise velocity is taken as
0.1c, as suggested by the results Of the Project
Daedalus study [6]. The probe construction time t is estimated as 10 years for nonreproducing probes
[6] and 100 years for reproductive devices [2]. Residence time a, the time required to fully
explore the target system, arbitrarily 15 taken to be 1 year. The number of
alien star systems, N(T), for which complete reports
are received by the sending civilization by the end of a Galactic Disk
exploration programme of duration T. is shown in
Figure 1 for nonreproducing and reproducing probe strategies.
As seen in Figure 1, Bracewell probes, which visit only one star (n = 1), return information to the sending civilization at a faster rate than reproducing starprobes for exploratory programmes involving less than 1000 stars corresponding to a distance of ~100 light-years in the Galactic Disk. For comparatively brief exploration programmes (T <= 104 years) having limited objectives, Bracewell probes outperform reproductive automata and nonreproductive starprobes with n > 1.
However, for longer term programmes (T > 104 years), n must increase if nonreproducing probes are to compete effectively with reproducing probes. For any given programme duration T these exists some optimum value of n such that N(T) is a maximum, though the choice of this n will inevitably result in slower rates of information return at the outset since the travel time between exploration cells becomes longer for greater n. Nonreproducing starprobes with large values of n compete successfully because such a strategy, in effect, simulates an immortal Bracewell probe, a "minimally reproducing" (m = 1) device. But even for n® ? nonreproducing starprobes are less effective than reproducing automata for exploration programs involving more than 106 stars to distances beyond ~1000 light-years in the Galactic Disk.
Launching more than one initial self- reproducing starprobe does not much alter the above conclusions. If Z such automata are created and dispatched, the performance improves by at most a factor of Z. The actual improvement is somewhat less than this, since each new probe constructed by the sending society must spend additional time travelling to some more distant exploration supercell, whereas daughter probes built by reproducing automata already on station need not wait the extra time.
Figure 2 illustrates the effects of varying the mean interstellar cruise velocity. Nonreproducing and reproducing strategies are compared for V=0.01c, V=0.1c, and V=0.5c. The conclusions reached earlier are not much affected by the choice of velocity, although higher speeds apparently favour the reproducing strategy slightly. Stellar number density and cruise velocity are related because they both scale the travel time between stars. Hence the effects of increasing r are much the same as those of increasing V. In Figure 2, the curves for V=0.01c, V=0.1c, and V=0.05c for stellar densities in the Galactic Disk are virtually indistinguishable from those in which the Halo, Disk, and Core densities are used with V=0.1c.
Figure 3 demonstrates the effects of different building times t for nonreproducing starprobes.
Although the dependence is rather strong (N(T) µ t-1), our analysis of the relative merits of
the two galactic exploration models again is unchanged. For n = 1, reproducing probes are still superior to
nonreproducing devices beyond ~100 light-years for t = 1, 10, or 100 years. (The asymptotic behaviour
of the nonreproducing model for large T is given
approximately by N » nT/t.)
Also shown in Figure 3 is a decrease in the reproduction time b to 50 years, a projection
difficult to defend on the basis of current technology [2]. However, even this
much reduction in b yields
only 1-2 orders improvement in N(T), leaving the
basic conclusions unaffected once again.
There exist distinct regimes of operation for reproducing and nonreproducing starprobes. We find that reproducing devices are generally favoured for long exploration programme durations T, in regions of high stellar number density r, when the best interstellar cruise velocity V available is high, when building time t is comparatively long, or when advanced technology permits a shorter reproduction time b. Conversely, nonreproducing probes are favored for short T, low r, low V, short t, and long b. Residence time a has little effect so long as a << r/V. As a general rule of thumb, we might therefore expect to receive nonreproducing starprobes from impulsive low-technology Halo civilizations and reproducing automata from more patient high-technology Core cultures.
The minimization of galactic exploration time most likely will involve some combination of all the factors mentioned above. The best design for general-purpose interstellar probes may include elements of reproductive and nonreproductive strategies in order to take best advantage of the unique features of each. For instance, starprobes may be designed as "facultative reproducers," replicating themselves after some number of stellar flybys have been accomplished or some other specific condition has been met. Depending on the level of commitment to interstellar exploration which the sending society is willing to make, some optimal combination of T, n, m, and G may be chosen as appropriate for the objectives of a given programme.
The preceding analysis of reproducing and nonreproducing models presumes that a policy of maximizing the information gained in a given exploration period will be followed by the sending civilization. While this is the ideal scientific criterion, a practical criterion is likely to involve economic factors. Thus a cost-effectiveness comparison is of interest. As a measure of the cost-effectiveness of an exploratory program of duration T we take the average expenditure for probe construction during the programme per star explored. For nonreproducing starprobes this quantity is given by
|
|
(20) |
where q is the cost of a nonreproducing probe. The corresponding quantity when the sending society builds and launches only one self-reproducing automaton of cost Q is
|
|
(21) |
A cost criterion thus leads to a choice of reproducing over nonreproducing probes when CE2 < CE1, yielding the requirement
|
|
(22) |
Estimates of Q/q (n = 1) are uncertain, but Freitas [2] has argued that the ratio is at least 100. A reasonable upper limit is 103. If the figure of Q/q» 100 is adopted then the criterion for the choice of reproducing over nonreproducing starprobe strategies favors programs in which the number of stars to be explored is ~100. This is less than the N ~ 103 stars based on the policy of maximum information return for n = 1. If, On the other hand, the figure of Q/q» 103 is adopted then the two criteria become roughly comparable. Thus, if a self-reproducing automaton is not greatly more expensive to build than a nonreproducing starprobe, then a cost effectiveness analysis gives the obvious result that building one reproducing probe is better than constructing a large number of non-reproducing devices to explore all but the nearest ~100 stars. In this case the amount of information obtained would not equal the non reproducing strategy (n = 1) until N ~ 103 stars. (See Figure 1.)
The threshold of effectiveness for self-reproducing probes varies from
102-106 stars depending on the details of the exploration
strategy and the criteria of effectiveness selected. However, in all cases the
preference for nonreproducing starprobes in nearby regions of space and
reproducing probes for more distant stars is a clear and persistent result. This
has implications for SETI searches for interstellar messenger craft. Any
nonreproducing alien probes discovered in the Solar System during the normal
course of future SETI research would most likely have been sent by
extraterrestrial civilizations located within ~1000 light-year radius of the
Sun, whereas any self- reproducing automata similarly detected probably
originated far outside this exploration sphere.