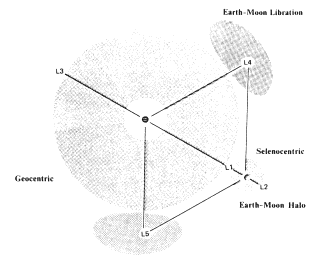
Fig.
1. Schematic of SETI orbital search regions for extraterrestrial messenger
probes, projected on the Earth-Moon plane.
Xenology Research Institute, 8256 Scottsdale Drive, Sacramento, California
95828
Received January 17, 1983; revised March 15, 1983
Icarus 55, 337-343 (August 1983)
0019-1035/83 $3.00
Copyright © 1983 by Academic Press, Inc.
All rights of reproduction in any form reserved.
Note: This web version is derived from an earlier draft of the paper and may possibly differ in some substantial aspects from the final published paper.
From an observational standpoint all extraterrestrial artifacts fall into one of three classes: (I) Objects intended to be found, (II) objects intended not to be found, and (III) objects for which detection by us is irrelevant or unimportant. The simplest assumption is that extraterrestrial technology is sufficient to guarantee the intended result. Thus class I objects cannot be present in the solar system because we have not observed their intentional manifestations. Class II objects may be present but it is impossible for us to observe them. Only class III objects may be observable.
The exploration goal restricts the search space for observable class III artifacts. These objects must elect to reside in the best possible location from which to monitor phenomena relevant to their mission. Earth is the only known site of life and intelligence in the solar system, so the simplest assumption is that the probe will recognize the fact and take up residence nearby, stationing itself in lunar or cislunar orbit. The Earth's surface is an unlikely site because of increased risk in the active and degradative terrestrial environment, more restricted access to solar energy, and the probe's impaired ability to continuously monitor the entire terrestrial and interplanetary environment during long-term studies.
The goal of long-duration exploration and the need to observe the Earth from space impose size constraints on possible messenger probes. First, an optical ground resolution y ≤ m is required for unambiguous visual detection from orbit of intelligent activity on the surface of the Earth (Shklovskii and Sagan, 1966). To resolve objects of dimension y at wavelength λ at a distance r from the extraterrestrial observer requires a diffraction-limited optical aperture of size ~(1.22)λr/y. From cislunar orbital space (70,000 < r < 384,000 km), this means a telescope size of ~3-30 m.
Second, an artifact must withstand catastrophic meteoroid impacts likely to occur during an on-orbit residence time t. The mass of a particle whose average flux across the surface of a cube of area 6L2 is unity after τ years in near-Earth space is approximated from the empirical data of Dohnanyi (1972, Fig. 1) as log (Mp) ~ log (τL2) - 6.7. A second empirical relation modified from Fujiwara (1980, Fig, 3) for the complete destruction of cubic rock targets by high-velocity frontal impact spallation is log (Mp) ~ log (2L2.5/V 2) + 7, where the smallest body which can survive an impact of energy (1/2)MpV2 is of size L. If artifact density and material strength are not grossly dissimilar from rock, then combining these empirical relations we have log (L) ~ log (V 4) + log (τ2) - 28 and the minimum size for defenseless artifacts is >0.2-20 m for a >105 to 106-year residence time (~ speciation timescale on Earth; Rensch, 1960) with V = 22 km/sec (Volkoff, 1966) in the vicinity of Earth.
Third, numerical integrations by Katz (1975) of the motion of objects placed at the triangular lunar libration points show that escape time is not much affected when radiation pressure force/gravitational force < 10-6. For radiation pressure in the geometrical optics case (Burns et al., 1979), this condition requires L > 0.2 m which also corresponds to an exponential decay time of >~109 year for artifacts in planetocentric orbits due to Poynting-Robertson drag alone. Cislunar bodies larger than 20 mm with velocities 0.3-3 km/sec are not lost from circumplanetary orbit by radiation pressure-induced perturbations of eccentricity (Burns et al., 1979).
Finally, exploration is useless unless the artifact can return information to its creators. Radio transmissions at waterhole frequencies 1-10 GHz are optimum in terms of bandwidth, energy cost, and background noise (e.g., Morrison et al., 1977; Billingham and Pesek, 1979). To achieve a gain of 1 < g < 107 (~ Arecibo) requires a minimum waterhole antenna diameter ~ (λ/π) g1/2 = 0.01-30 m.
These considerations suggest that a reasonable search limit is an artifact of
typical dimension ~1-10 m with a visual geometric albedo of ~-0. 1 (pv = 0.02-0.35 for asteroids), termed the
limiting artifact.

Fig.
1. Schematic of SETI orbital search regions for extraterrestrial messenger
probes, projected on the Earth-Moon plane.
Geocentric orbits. Cislunar geocentric orbits with apogees beyond the mean distance of the interior collinear Earth-Moon Lagrangian point L1 (326,000 km) lack long-term stability and thus are unsuitable as parking orbits. Szebehely (1980) suggests a maximum stable radius for planar circular orbits of 244,000 km, a more restrictive limit. Orbits with perigees below 5500 km altitude have lifetimes less than 106 years due to atmospheric drag, whereas perigees above 8000 km yield lifetimes comparable to the age of the solar system (Perini, 1975). Perigees between 3000 and 64,000 km altitude in the Van Allen radiation belts are unlikely because of the increased potential risk (e.g., to electronic systems: Ziegler and Lanford, 1979) for long-duration missions. The translunar Earth-Moon barycentric orbital volume lying between Earth-Moon L2 (449,000 km) and Sun-Earth L1 (1.49 x 106 km) while apparently quite large appears stable only in a very restricted range of radii, if at all (Harrington, 1977; Szebehely, 1980; Markellos and Roy, 1981), and also is unattractive because of its greater distance from Earth. Hence the most plausible search volume lies roughly between two geocentric spheres of radii 70,000 km and 326,000 km, with Earth-relative velocity limits 1.1-3.4 km/sec, search area S = (360)2/π deg2, and total apparent angular rate range Δw= 5.2 x 10-3 deg/sec.
Detection of a limiting artifact requires visual magnitude limits from +15 (70,000 km) to +18 (326,000 km). Existing military radars such as the Altair radar at Kwajalein Missile Range monitor the geocentric volume to 40,000 km for 5-m objects, but none of these pencil-beam radars is effective for search. The new GEODSS (ground-based electro-optical deep space surveillance) system which replaces the SAO Baker-Nunn network can detect + 16.5-mag near-Earth satellites but has not been employed for significant asteroid searches and cannot perform well at the required limiting sensitivity. The most comprehensive work is by Tombaugh et al. (1959) in a 5-year program during which 15,567 photographs were taken in an attempt to discover small natural Earth satellites. The search was confined entirely to the ecliptic and equatorial planes, with excellent coverage below 10,000 km altitude to magnitude +15. However, in the cislunar SETI region Tombaugh searched only three concentric circular orbital zones along the ecliptic-85,000 km retrograde (173o coverage), 88,000 km direct (342o coverage), and 121,000 km retrograde (158o coverage). Even if the search could be deemed complete out to Earth-Moon L1 within ± 5o (Tombaugh's Schmidt field) of the ecliptic, 90% of the search volume would remain unexamined for any serious magnitude limit.
Selenocentric orbits. Stable selenocentric orbits cannot have apolunes greater than the mean distance between the Moon and Earth-Moon L1 (58,100 km). Szebehely (1980) and Markellos and Roy (1981) give the maximum stable radii for planar circular stable orbits as 28,000 and 16,700 km for direct and retrograde satellites, respectively. Perilune is only weakly constrained by interaction with the present lunar atmosphere, though Chernyak's (1978) suggestion of a possible ancient ≤5 x 10-7 bar lunar atmosphere could increase minimum altitude to several thousand kilometers. Hence the selenocentric orbital search volume lies between 3000 and 58,100 km, angular diameter 17o (S = 230 deg2) viewed from Earth, with velocity limits 0.3-1.8 km/ sec relative to the Moon (Δw = 5.4 x 10-4 deg/sec).
Ground-based detection of a limiting artifact requires a visual magnitude limit of +18 to +19. Pickering (1890) searched a 30o x 30o square swath to magnitude +10 during lunar eclipse, which Barnard (1895) extended to magnitude +12. Tombaugh et al. (1959) performed a multitelescopic survey during lunar eclipse of a 19o circular field to magnitude +13, save a small region near the Earth-Moon axis where the limit was +12. Zones of maximum elongation within 5o of the lunar orbital path were probed to magnitude + 14 to +17.
Earth-Moon libration orbits. In the classical three-body problem, small objects placed at one of the five Lagrangian points in the plane of revolution are in dynamical equilibrium, and two of these, the triangular points L4 and L5, are stable. The true Earth-Moon system represents a four-body problem because of the significant gravitational influence of the Sun. L4 and L5 themselves are unstable, but large, stable libration orbits around them, synchronized with the synodic month, have been shown analytically (Schechter, 1968; Kamel, 1969) and numerically (Kolenkiewicz and Carpenter, 1968) to exist. Thus, the positions of objects in the stable libration orbits can be computed and unique time-variable ephemerides determined. Each synodic libration orbit has two stable phases 180o apart with semimajor axis 150,000 km and semiminor axis 75,000 km. Oscillations in the Earth-Moon plane are likely for objects parked for very long periods of time, but deviations from the solar-synchronized positions should be minimal for powered artifacts inserted on precision trajectories. Out-of-plane motion is not seriously excited by the Sun and is almost certainly less than the mean lunar/ecliptic inclination (Roosen et al., 1967; Schechter, 1968; Schutz and Tapley, 1970; Katz, 1975; Tilton, 1980). Thus, the three-dimensional search volume near L4/L5 is a squat, elliptical cylinder, measuring 300,000 x 150,000 km in the lunar orbital plane and extending at most 35,000 km above and below the plane, with velocity limits 0.7-1.3 km/sec relative to the Earth, S = 900 deg2 for both regions, and Δw = 1.1 x 10-4 deg/sec.
Detection of a limiting artifact requires a comprehensive search to magnitude +18 to +19. The regions near L4/L5 have been examined for luminous dust clouds following reports of their existence by Kordylewski (1961, 1971), Simpson (1967), Allen et al. (1967), Roach et al. (1973), Munro et al. (1975), and Roach (1975). These investigations covered less than the full 450-deg2 search space near each libration point to limiting magnitudes < +10 and failed to confirm the discovery (Wolfe et al., 1967; Roosen, 1968; Weinberg et al., 1969; Morris, 1971; Schlosser et al., 1975; Shoemaker, 1982, personal communication).
Kordylewski also searched the entire region for discrete objects to magnitude +12; Bruman (1969) examined a 44-deg2 field near L4 during lunar eclipse using the 48-in. Palomar Schmidt to limiting magnitude +15 to +17; Giclas (Tombaugh, 1981, personal communication) searched a 180-deg2 field near L5 to magnitude +16; and Freitas and Valdes (1980) performed a preliminary survey near the L4/L5 synodic libration orbits to magnitude +14 -- all with negative results. An informal radar search near L4/ L5 conducted at Arecibo found no targets > 10 m2 (Jurgens, 1967). Valdes and Freitas (1983) photographed the entire 45o libration orbit region within ± 2.5 deg of the lunar orbital plane near L4/L5 to limiting magnitude +17 to +19 for a limited range of artifact velocities using the 24-in. Warner & Swasey Schmidt telescope at KPNO, but found nothing.
Earth-Moon halo orbits. Periodic halo orbits near the collinear Lagrangian points L1 and L2 have long been known to require station-keeping due to their dynamic instability (Farquhar, 1970), but Breakwell and Brown (1979) have demonstrated the theoretical existence of families of stable nonplanar orbits. The inclusion of lunar eccentricity ruins the stability, but Breakwell (1980, personal communication) believes there is a good chance real stable halo orbits exist. These families lie entirely within a rectangular hexahedral Moon-centered volume measuring 80,000 x 80,000 km in the lunar orbital plane and 160,000 km in vertical extent. Typical halo object velocity is 0.8 km/sec relative to the Moon, with Δω = 2.8 x 10-4 deg/sec.
The rectangular search space of S = 280 deg2 overlaps considerably with the selenocentric space, representing an additional 90 deg2. Pickering (1890) surveyed this additional space to magnitude +10, and Tombaugh et al. (1959) examined about half to magnitude +13. This search is similar to the selenocentric survey except for the anticipated slower motion of halo objects as compared to lunar satellites.
The calendar search time is Tc = To/k, and we assume a reasonable search program is Tc ≤ 2 years per orbital region. The wide-field Palomar Schmidt telescope has f = 44 deg2, Δt = 900 sec, V1 = +21 mag, Δa = 3 x 10-4 deg (~ 1 arcsec seeing), and k = (8 hr/24 hr)(10%) = 0.03 is a plausible usage figure. For Palomar Schmidt searches with Tc = 2 years and Ps = 0.99, each orbital region except geocentric may be searched for 0.1-albedo objects to R ~ 3-5 m, and the geocentric region to ~40 m. These limits assume a random search pattern, hence are pessimistic since Tc down to a given R may be improved using optimal search techniques (Stone, 1975) by taking full account of orbital mechanics exclusions as each position-velocity element is examined. Tc may also be improved if part of the search is performed in parasitic or serendipity-data mode concurrent with other non-SETI programs which effectively increases the value of k. A space-based wide-field telescope with characteristics similar to the Palomar Schmidt but with V1 = +24 could search each orbital region except geocentric to ~1 m, and geocentric to ~10 m, for k = 0.03, Tc = 2 years.
Artifacts plausibly might also be detectable in the infrared. Cislunar objects in equilibrium with the insolation having a bolometric emissivity ~0.1 and a Bond albedo ~0.1 have a temperature ~390 K and infrared magnitude N = +11 at lunar distance and N = +7 to +10 in the geocentric region for R = 1 m at 10 mm (Morrison, 1977; Hansen, 1977). The AFCRL 11 mm sky survey achieved N = 0 to -1 (Lebofsky et al., 1978), a limit of ~100-300 m. and the IRAS orbiting telescope should reach N = +7 to +8 at 10 mm (Aumann kind Walker, 1977), a limit of ~3-6 m for all orbital regions after Tc = 0.25 year. However, these limits may not be secure. Selection criteria for the final AFGL catalog were chosen to exclude asteroids and satellites. IRAS has a mission lifetime of less than I year and the original IRAS software was designed to reject asteroids (Morrison and Niehoff, 1979), although now a specialty database for fast-moving asteroids evidently will be established (Thomas, 1983).
The author thanks Ronald N. Bracewell, Robert S. Harrington, Michael D. Papagiannis, Robert G. Roosen, Clyde W. Tombaugh, Francisco Valdes, George W. Wetherill, and an unnamed referee for their comments on an earlier version of this manuscript. This research was supported by the Xenology Research Institute.
Aumann, H. H., and R. G. Walker (1977). Infrared astronomical satellite. Opt. Eng. 16, 537-543.
Barnard, E. E. (1895). On a photographic search for, a satellite to the Moon. Astrophys. J. 2, 347-349.
Billingham, J., and R. Pesek, Eds. (1979). Communication with Extraterrestrial Intelligence. Pergamon, Oxford.
Bracewell, R. N. (1960). Communications from superior galactic communities. Nature 186, 670-67 1.
Bracewell, R. N. (1975). The Galactic Club: Intelligent Life in Outer Space. Freeman, San Francisco.
Breakwell, J. V., and J. V. Brown (1979). The 'halo' family of 3-dimensional periodic orbits in the Earth-Moon restricted 3-body problem. Celest. Mech. 20, 389-404.
Bruman, J. R. (1969). A lunar libration point experiment. Icarus 10, 197-200.
Burns, J. A., P. L. Lamy, and S. Soter (1979). Radiation forces on small particles in the Solar System. Icarus 40, 1-48.
Chernyak, Yu. B. (1978). On recent lunar atmosphere. Nature273, 497-501.
Dohnanyi, J. S. (1972). Interplanetary objects in review: Statistics of their masses and dynamics. Icarus 17, 1-48.
Farquhar, R. W. (1970). The Control and Use of Libration Point Satellites. NASA TR R-346.
Freitas, R. A., Jr, (1980a). Interstellar probes; A new approach to SETI. J. Brit. Interplanet. Soc. 33, 95-100.
Freitas, R. A., Jr. (1980b). A self-reproducing interstellar probe. J. Brit. Interplanet. Soc. 33, 251-264.
Freitas, R. A., Jr. (1983). The search for extraterrestrial artifacts (SETA). Submitted for publication.
Freitas, R. A., Jr., and F. Valdes (1980). A search for natural or artificial objects located at the Earth-Moon libration points. Icarus 42, 442-447.
Fujiwara, A. (1980). On the mechanism of catastrophic destruction of minor planets by high-velocity impact. Icarus 41, 356-364.
Hansen, O. L. (1977). An explication of the radiometric method for size and albedo determination. Icarus 31, 456-482.
Harrington, R. S. (1977). Planetary orbits in binary stars. Astron. J. 82, 753-756.
Jurgens, R. (1967). Search at Lagrangian points. Cornell University Research Report RS-70, pp. 76-77. AFOSR Contract AF-49(658)-1156 31 January 1967.
Jurgens, R. F., and D. F. Bender (1977). Radar detectability of asteroids: A survey of opportunities for 1977 through 1987. Icarus31, 483-497,
Kamel, A. A. (1969). Perturbation Theory Based on Lie Transforms and Its Application to the Stability of Motion Near Sun-Perturbed Earth-Moon Triangular Libration Points. Ph.D. dissertation, Stanford University, Stanford, Calif.
Katz, J. I. (1975). Numerical orbits near the triangular lunar libration points. Icarus 25, 356-359.
Kolenkiewicz, R., and L. Carpenter (1968). Stable periodic orbits about the Sun-perturbed Earth-Moon triangular points. AIAA J.6, 1301-1304.
Kordylewski, K. (1961). Photographic investigations of the libration point L5 in the Earth-Moon system. Acta Astron. 11, 165-169 [In German]. Air Force Cambridge Research Laboratories, Research Translation E-T-G-64-35.
Kordylewski, K. (1971). The dust ring of the Earth. Probl. Kosm. Fiz. 6, 164-167 [in Russian].
Lebofsky, J. J., D. G. Sargent, S. G. Kleinmann, and G. H. Rieke (1978). An observational study of the AFCRL infrared sky survey. Astrophys. J. 219, 487-493.
Markellos, V. V., and A. E. Roy (1981). Hill stability of satellite orbits. Celest. Mech. 23, 269-275.
Morris, E. C. (1971). Spaceborne Earth-Moon libration regions photography during Gemini 12 flight. In The Gemini Program: Physical Science Experiments Summary, pp. 71-75. NASA Manned Spacecraft Center.
Morrison, D. (1977). Asteroid sizes and albedos. Icarus 31, 185-220.
Morrison, D., and J. Niehoff (1979). Future exploration of the asteroids. In Asteroids (T. Gehrels , Ed.), pp. 227-237. Univ. of Arizona Press, Tucson.
Morrison, P., J. Billingham, and J. Wolfe, Eds. (1977). The Search for Extraterrestrial Intelligence, SETI. NASA SP-419.
Munro, R. H., J. T. Gosling, E. Hildner, R. M. MacQueen, and C. L. Ross (1975). A search for forward scattering of sunlight from lunar libration clouds. Planet. Space Sci. 23, 1313-1321.
Perini, L. L. (1975). Economical scheme for estimating orbital lifetimes. J. Spacecraft and Rockets 12, 323-324. See Errata, J. Spacecraft and Rockets 13, 64, 1976.
Pickering, E. C. (1980). Photographic search for a lunar satellite. In Miscellaneous Researches made during the years 1886-1890. Ann. Astron. Obs. Harvard Coll. 18, 77-83.
Rensch, B. (1960). Evolution Above the Species Level. Columbia Univ. Press, New York.
Roach, J. R. (1975). Counterglow from the Earth-Moon libration points. Planet. Space Sci. 23, 173-181.
Roach, F. E., B. Carroll, J. R. Roach, and L. H. Aller (1973). A photometric perturbation of the counterglow. Planet. Space Sci. 21, 1185-1189.
Roosen, R. G. (1968). A photographic investigation of the Gegenschein and the Earth-Moon libration point L5. Icarus 9, 429-439.
Roosen, R. G., R. S. Harrington, W. H. Jeffreys, J. W. Simpson, and R. G. Miller (1967). Doubt about libration clouds. Phys. Today 20, 5, 10-15.
Schechter, H. B. (1968). Three-dimensional nonlinear stability analysis of Sun-perturbed Earth-Moon equilateral points. AIAA J.6, 1223-1228.
Schlosser, W., H. M. Maitzen, and D. Hablick (1975). Upper limits for brightness and dust concentration of the hypothetical libration cloud at L4 in the system Earth-Moon based on photographic surface photometry. Astron. Astrophys. 45, 197-202.
Schutz, B. E., and B. D. Tapley (1970). Numerical studies of solar influenced particle motion near the triangular Earth-Moon libration points. In Periodic Orbits, Stability and Resonances (G. E. O. Giacaglia, Ed.), pp. 128-142. Reidel, Dordrecht, Holland.
Shklovskii, I. S., and C. Sagan (1966). Intelligent Life in the Universe. Holden-Day, New York.
Simpson, J. W. (1967). Dust cloud moons of the Earth. Phys. Today 20, 39-46.
Stephenson, D. G. (1982). Models of interstellar exploration. Q. J. Roy. Astron. Soc. 23, 236-251.
Stone, L. D. (1975). Theory of Optimal Search. Academic Press, New York.
Szebehely, V. (1980). Stability of planetary orbits in binary systems. Celest. Mech. 22, 7-12.
Thomas, G. R. (1983). IRAS preliminary science analysis at the OCC. J. Brit. Interplanet. Soc. 36, 38-42.
Tilton, H. A. (1980). Three-Dimensional Orbital Stability about the Earth-Moon Equilateral Libration Points. M.S. thesis, Air Force Institute of Technology, Wright-Patterson AFB, Ohio.
Tipler, F. J. (1981). Extraterrestrial intelligent beings do not exist. Phys. Today 34, 70-71.
Tombaugh, C. W., J. C. Robinson, B. A. Smith, and A. S. Murrell (1959). The Search for Small Natural Earth Satellites: Final Technical Report. Physical Science Laboratory, New Mexico State University, Las Cruces, New Mexico.
Valdes, F., and R. A. Freitas, Jr. (1983). A search for objects near the Earth-Moon Lagrangian points. Icarus 53, 453-457.
Volkoff, J. J. (1966). System protection requirements for the resistance of meteoroid penetration damage. J. Spacecr. Rockets3, 26-34.
Weinberg, J. L., D. E. Beeson, and P. B. Hutchison (1969). Photometry of lunar libration regions. Bull. Amer. Astron. Soc.5, 210-233.
Wolfe, C., L. Dunkelman, and L. C. Haughney (1967). Photography of the Earth's cloud satellites from an aircraft. Science 157, 427-429.
Ziegler, J. F., and D W. A. Lanford (1979). Effect of cosmic rays on computer memories. Science 206, 776-788.
Creation date: July 26, 1998
Last Modified: April 29, 1999
HTML Editor: Robert J. Bradbury
Revised and corrected by Robert A. Freitas Jr., 19 November 2002