A Search for Natural or Artificial Objects Located at the Earth-Moon Libration Points

The Earth-Moon system also has triangular libration points. However, in the Earth-Moon case the problem of stability is greatly complicated by the appreciable solar gravitational influence. Taking this properly into account, it can be shown theoretically and numerically that L4 and L5 are no longer stable. For instance, a detailed numerical integration of the motion of objects initially at rest in the Lagrangian orbits was performed by Schutz and Tapley (1970) They found large oscillations on the order of the Earth-Moon separation. For a object begun at L4 this led to a close lunar encounter with subsequent ejection from the system after 579 days.

Though the Lagrangian points are not stable, large stable orbits around the libration points have been determined analytically by Schechter (1968) and Kamel (1969) and numerically by Kolenkiewicz and Carpenter (1968). Schechter found one stable orbit using a second-order perturbation .procedure and assuming a circular lunar orbit. The stable orbit was synodic with the Sun. In addition he found that oscillations out of the lunar orbital plane were essentially decoupled from the in-plane motion. The numerical search by Kolenkiewicz and Carpenter, using restricted coplanar motion and eccentric lunar orbits, found two synodic stable orbits of similar size with a 180' phase difference. The scale of the orbits found by Schechter and by Kolenkiewicz and Carpenter differed because of the low-order analytic technique. Kamel used a third- and fourth-order theory in the coplanar model, the third-order analysis including an eccentric lunar orbit, which agreed well with the numerical results. A schematic of these stable "halo orbits" is shown in Fig. 1.

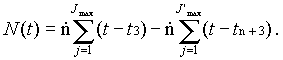
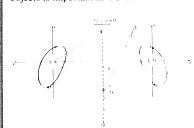
Fig. 1. Schematic diagram of the Earth-Moon triangular libration points L4 and L5. and their associated halo orbits, in the rotating coordinate system de scribed by Kamel (1969). Coordinates x and y are in units of the mean Earth-Moon separation.
 
 

To the best of our knowledge, no observations of the Earth-Moon halo orbits have yet been attempted, nor have searches specifically designed to detect discrete objects at L5 been reported in the literature. Investigation of these positions for trapped objects is important as a check on theoretical calculations, for the discovery of asteroidal material, and as a SETI (Search for Extraterrestrial Intelligence) search for possible alien artifacts. The authors have attempted a preliminary photographic search with the 30-in. Cassegrain telescope at Leuschner Observatory in Lafayette, California.

The SETI aspect of this observational search is based on the proposals that the Earth-Moon libration points might represent excellent parking orbits for SETI receiver antennae (Basler et al., 1977), for large space habitats (O'Neill, 1977), or for interstellar probes sent to the Solar System by advanced technical societies located elsewhere in the Galaxy (Lawton, 1974). The possibility of using messenger probes in the search for extraterrestrial intelligence was first suggested by Bracewell (1960), and the feasibility of this approach recently has been demonstrated by the British Interplanetary Society Starship Study (Martin, 1978). Much like the "preferred frequency" concept in SETI beacon theory, libration orbits might constitute the most universally convenient meeting places for alien spacecraft exploring arbitrary stellar systems. A viable long-term SETI program may be founded upon a search for these objects (Freitas, 1980a).

We suggest (Freitas, 1980b), that halo orbits could be among the best places to begin a search for evidence of ancient spacecraft parked in the Earth-Moon system. Such orbits should be stable over geological time scales and are expected to be widely available in arbitrary solar systems that might be visited by exploratory spacecraft (Szebehely, 1967; Everhart, 1973; Weissman and Wetherill, 1974). In addition, libration/halo orbits may serve as well-defined loci for a network of interplanetary surveillance and communication relay stations (Strong, 1967; Farquhar, 1971).
 

The equation for halo orbits about L4 in the (x, y) coordinate system defined in Fig. 1 is given by Kamel (third-order orbits e₂ and e₃ with lunar orbital eccentricity e = 0.0549) as

Kamel's halo orbits were calculated from (1) by using i, a_i, and b_i provided in Table I to generate the Lagrangicentric orbital coordinates (f = x, f = y) as a function of q_s, and q_e. The angle q_s. between the Sun and the Moon was taken as the apparent angle in the sky, since a trial projection of the Sun onto the lunar orbital plane produced only a negligible correction to the computed halo orbits. The angle q_e, between the Moon and its point of perigee was determined by linear interpolation of the preceding and succeeding ephemeris perigee positions to the date of observation. Calculations of halo orbits about L5 were performed by reflecting the (x-y) coordinate system about the y-axis and reversing the time dependence. This is indicated by the coordinate axis at L5 in Fig. 1.

The mean motion of an object in an L4/L5 halo orbit is synchronized with the synodic month (Kolenkiewicz and Carpenter, 1968; Schechter, 1968). Thus, it is possible to determine a unique time-variable position for trapped bodies or hypothetical ancient spacecraft. The sky positions of the triangular libration points and the four unique synodic halo points were computed using the American Ephemeris and Nautical Almanac 1979 at every hour during the planned observing periods in August-September 1979, and were interpolated to 1-min intervals to permit close digital tracking.

To obtain the best possible conditions, the search was conducted close to maximum reflection angle to ensure full brightness from any objects that might be present. About half the photographs were taken in a moonless sky. The remainder were taken before moonset, as early (for L4) and as late (for L5) in the Moon's phases as possible, consistent with the above reflection angle requirement. The exposures were made by manually guiding the telescope in declination and by adjusting the tracking oscillator continuously according to digital readouts. No visual target was available, so guiding was unavoidably imperfect. Conservatively, libration/halo objects may have trailed as much as 1^s in right ascension and 15" in declination during each exposure, thus decreasing the limiting magnitude. Seeing was generally 3-8" which further reduced the visual magnitude limit.

It is likely that the true position of orbiting halo objects is very near the coplanar solution. The out-of-plane halo orbit motion studied by Schechter (1968) was found not to be seriously excited by the Sun. Roosen et al. (1967) estimated an oscillation perpendicular to the Earth-Moon plane with a period equal to the synodic period and an amplitude as seen from the Earth of about 0°.25, and concluded that the integrated effect of the Sun would be to smear any material into bands lying in the plane of the lunar orbit. For particles initially at the triangular libration point L5 Schutz and Tapley (1970) found a progressive reduction in inclination from the mean lunar value of 5°.15 down to a lower limiting value of about 2° after 5000 days, a trend which they were unable to explain.

The search for objects at the Lagrangian points and in the halo orbits given by (1) allowed for excursions of up to 1° away from the orbital plane and tip to 8° along the plane of the orbit. The circular field of the Leuschner telescope is 1°. Photographs were taken at points along the orbital plane and at positions offset by 0°.5 to survey a 2^o square grid around each point. These observations covered only about 6° along the halo plane at intervals of about 2°. A similar sampling was made in the vicinity of the Lagrangian points L4 and L5. Given the limited sensitivity and narrow field of each photograph this search must be considered preliminary and is not complete.

Each photograph consisted of a 10-min exposure, then a 1-sec "jog" obtained by briefly disengaging the telescope drive, followed by another 10-min exposure on the same film. Any libration/halo objects thus would appear as doublets on each exposure, helping to eliminate most of the false alarms caused by defects in the photographic emulsion. Observations took place during 1-4 August 1979, 14-17 August 1979, 29-31 August 1979, and 11-13 September 1979. A total of 90 photographs was taken, including 41 at L4 and its associated halo orbit positions and 40 similarly near L5. All were 4 x 5 in. (100 x 130 mm), Tri-X ASA 320 sheet film, firmly affixed to rigid glass plates during exposure and developed with manual agitation for 5 min in D-19. Nine calibration photographs were taken of M15, a prominent and well-studied globular cluster, covering a variety of observing conditions.

The authors would encourage others to perform more comprehensive observational investigations of this type with the possibility in mind of ancient artifacts in the Solar System. Our experience suggests such work could most profitably be accomplished using a wide field, wide aperture Schmidt telescope which would push the limiting magnitude to about +21. This corresponds roughly to an object at the distance of the Moon having the size of Pioneer 10 and an albedo like that of carbon black.